Сборник алгебраических задач для 8-го и 9-го классов - часть вторая (Шапошников, Вальцов) 1935 год - старые учебники

§ 9. Уничтожение иррациональности в знаменателе дроби (15)

§ 10. Квадратный корень из двучлена вида (16)

§ 11. Задачи на все действия над радикалами (17)

§ 12. Степени и корни с дробными показателями (18)

§ 13. Мнимые числа (20)

106.В уравнении х2— 6х-}-^ = 0 определить то значение при котором корни уравнения а и 0 удовлетворяют зависимости За 4- 20 = 20.

107.В уравнении л8— 5х 4-^ = 0 определить то значение д, при котором корни уравнения а и 0 удовлетворяют зависимости За4-50=17.

108.Какая зависимость должна существовать в уравнении л2 -|-рх -|- д = 0 между коэфициентами р и д, чтобы один корень этого уравнения был в т раз более другого?

109.В формуле решения уравнения х2 4“Рх 4“ 7 = 0 уничто¬жить иррациональность в числителе дроби.

§ 3.Составление буквенных квадратных уравнений.

110.Найти два числа, произведение которых р, а частное д.

111.При делении одного числа на другое в частном получается айв остатке Ь; произведение этих двух чисел равно с. Найти эти числа.

112.Разложить число а на два множителя, разность между которыми равна Ь.

113.Найти два числа, сумма квадратов которых .9, а отноше¬ние р'.д.

114.Сумма правильной дроби с обратной равна а. Найти ве¬личину дроби; определить, при каких значениях а задача имеет решение.

115.Одна часть суммы в а руб. приносит ежегодно Ь руб., а другая с руб. прибыли. По скольку процентов прибыли дает каж¬дая часть, если со второй получается одним процентом больше, чем с первой?

116.Отрезок длиною а разделен на две части, из коих одна есть средняя пропорциональная между всем отрезком и второй частью. Определить длины частей отрезка.

117.Разделить прямолинейный отрезок длиною а на такие две части, чтобы удвоенная площадь квадрата, построенного на одной части, равнялась площади прямоугольника, измерениями которого служат другая часть и сам данный отрезок.

118.Периметр прямоугольника равен 2р, площадь равна 5. Определить стороны прямоугольника; исследовать решение и вы¬яснить, при каком соотношении между р и 5 прямоугольник обращается в квадрат.

119.В равнобедренном треугольнике боковая сторона равна л, а высота менее основания на т. Найти основание и высоту равно¬бедренного треугольника.

120.В прямоугольном треугольнике из вершины прямого угла опущен на гипотенузу перпендикуляр. Определить части, на которые этот перпендикуляр делит гипотенузу, если длина перпендикуляра А, а гипотенузы — с.

121.Вели радиус круга увеличить на а сантиметров, то площадь круга увеличится в п раз. Определить радиус круга.

122.По сторонам прямого угла от его вершины в одно и то же время начинают двигаться два тела. Скорость одного У1 сантимет¬ров в секунду, скорость другого У3 сантиметров в секунду. Через сколько времени расстояние между этими телами будет равно Л сантиметров?

123.Равнодействующая двух сил, приложенных к точке под углам в 120°, равна Р; отношение этих сил т:п. Определить со¬ставляющие силы.

124.Электрическая лампа в т свечей висела над столом. Когда она перегорела, ее заменили лампой в п свечей и, чтобы степень освещения не изменилась, опустили на А сантиметров. На какой высоте над столом висит теперь лампа?

125.Два магнита А и В находятся на расстоянии Л сантимет¬ров друг от друга. Магнит В в п раз сильнее магнита А. На каком расстоянии от магнита А находится точка, в которой притяжение обоих магнитов одинаково, если известно, что сила притяжения магнита обратно пропорциональна квадрату его расстояния от при-тягиваемого тела?

126.Две водопроводные трубы с диаметрами а и А надо заме¬нить одной трубой с той же пропускной способностью. Каков дол¬жен быть диаметр этой трубы?

127.Камень падает в колодец, и звук его падения наблюдатель услышал через п секунд после начала падения. Найти глубину ко¬лодца, если скорость звука равна 330 ж в секунду и ^=9,8 м в секунду.

128.Из прямоугольного куска жести, измерения которого а н А, требуется сделать открытую коробку так: 1) чтобы площадь стенок равнялась площади дна, 2) чтобы площадь дна имела заданный размер $. Выяснить условия годности корней.

129.Железнодорожный путь имеет длину а километров. Если увеличить скорость поезда на А километров в час, то поезд будет затрачивать на прохождение пути на с часов меньше, чем теперь. Сколько времени затрачивает поезд на прохождение всего пути и какова его скорость?

130.Два автомобиля выезжают одновременно из места А в место В. Один из них проходит в час на т километров больше, чел» другой, и поэтому приходит в место В на л часов раньше другого. Расстояние между А и В равно Р километрам. Сколько километ¬ров проходит в час каждый автомобиль?

131.Два прокатных стана могут, работая одновременно, про* катать а килограммов железа в Т часов. Если будет работать только первый из станов, то на прокатку указанного количества железа потребуется на I часов больше времени, чем при работе одного второго стана. Во сколько времени может прокатать а килограммов железа каждый из станоз, работая отдельно?

§4. График квадратной функции. Графическое решение квадратного уравнения.

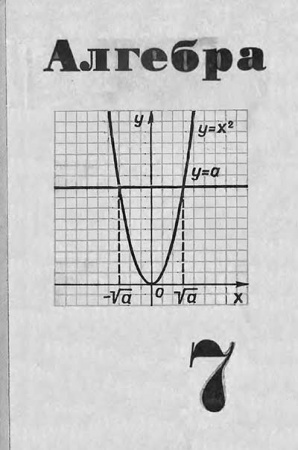
График уравнения у —ах2 есть парабола, касающаяся оси X в точке О и симметрично расположенная относительно оси К Если а>0, то парабола у—ах3 проходит по ту сторону от оси X, по какую лежат положительные значения ординат; если а<^0, то, на* оборот, парабола проходит по ту сторону оси Л, по какую лежат отрицательные значения ординат.

График уравнения у = ах3 Ьх -|- с есть парабола, ось которой параллельна оси У и ветви которой направлены в положительном или отрицательном направлении оси У, в зависимости от того, бу* дет ли й>0 иля а<^0.

Можно двумя способами графически решать квадратное уравнение.

Первый способ.

Построив по точкам параболу у = ах3 Ц- Ьх с, определяем корни уравнения ах3 Ьх -|- с = 0 как абсциссы точек пересечения параболы с осью X. Если парабола у = ах3 Ьх -|- с пересекает ось X в двух точках, то уравнение аха-|-&к4-а=0 имеет два различных действительных корня. Если парабола касается оси X, то уравнение имеет два равных действительных корня. Наконец, если парабола не пересекает оси X, то уравнение имеет два мнимых (сопряженных) корня (черт. 1).

Второй способ.

Перепишем уравнение ах3 Ьх -{- с = 0 в виде ах’ = — Ьх—с..

Полагая ах2=у, получим систему:

у=ах2; у = — Ьх — с.